2013长春赛区网络赛的1009题
比赛的时候这道题英勇的挂掉了,原因是写错了一个系数,有时候粗心比脑残更可怕
本题是关于Bell数,关于Bell数的详情请见维基:http://en.wikipedia.org/wiki/Bell_number
其中有一句话是这么说的: And they satisfy "Touchard's congruence": If p is any prime bumber then
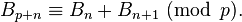
但95041567不是素数, 分解之后发现 95041567 = 31 × 37 × 41 × 43 × 47
按照上述递推式,利用矩阵快速幂可以得到 Bn mod p, (p = 31, 37, 41, 43, 47),因为p最大47,所以矩阵快速幂O(p^3 * log(n/p))不会超时,
当然要先利用以下公式把B1-B47预处理出来:
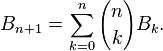
得到5个Bn mod p (p = 31, 37, 41, 43, 47)之后,怎样得到Bn mod Πp 呢?
利用中国剩余定理可以完美的解决上述问题
详情见代码:
#include#include #define MOD 95041567#define LL long longconst int maxn = 50; //必须加 const,否则编译错误LL x[5] = {31, 37, 41, 43, 47};LL X;class Matrix {public: LL val[maxn][maxn]; Matrix() { memset(val, 0, sizeof(val)); } Matrix operator*(const Matrix& c) const { Matrix res; for (int i = 0; i < X; ++i) for (int j = 0; j < X; ++j) for (int k = 0; k < X; ++k) { res.val[i][j] += val[i][k] * c.val[k][j]; res.val[i][j] = (res.val[i][j] + X) % X; //防止矩阵元素变为负数,若不需要,去掉"+MOD" } return res; } Matrix operator*=(const Matrix& c) { *this = *this * c; return *this; } Matrix Pow(LL k) { //返回one^k Matrix res = Zero(); Matrix step = One(); while (k) { if (k & 1) res *= step; k >>= 1; step *= step; } return res; } Matrix Zero() const { Matrix res; for (int i = 0; i < X; ++i) res.val[i][i] = 1; return res; } Matrix One() const { Matrix res; for (int i = 0; i < X - 1; ++i) res.val[i][i] = res.val[i + 1][i] = 1; res.val[0][X - 1] = res.val[1][X - 1] = res.val[X - 1][X - 1] = 1; return res; }};void gcd(LL a, LL b, LL& d, LL& xx, LL& y) { if (!b) { d = a, xx = 1, y = 0; } else { gcd(b, a % b, d, y, xx); y -= xx * (a / b); }}LL china(LL n, LL* a, LL* m) { LL M = 1, d, xx = 0, y; for (int i = 0; i < n; ++i) M *= m[i]; for (int i = 0; i < n; ++i) { LL w = M / m[i]; gcd(m[i], w, d, d, y); xx = (xx + y * w * a[i]) % M; } return (xx + M) % M;}LL c[50][50], f[50], a[5];int main() { int T; for (int i = 0; i < 50; ++i) { c[i][0] = c[i][i] = 1; for (int j = 1; j < i; ++j) c[i][j] = (c[i-1][j] + c[i - 1][j - 1]) % MOD; } f[0] = 1; f[1] = 1; for (int i = 2; i < 50; ++i) { for (int j = 0; j < i; ++j) f[i] = (f[i] + c[i - 1][j] * f[j]) % MOD; } scanf("%d", &T); while (T--) { LL n; scanf("%I64d", &n); if (n < 50) { printf("%I64d\n", f[n]); continue; } memset(a, 0 ,sizeof(a)); for (int i = 0; i < 5; ++i) { X = x[i]; Matrix m; m = m.Pow(n / X); for (int j = 0; j < X; ++j) a[i] = (a[i] + f[j] * m.val[j][n % X]) % X; } printf("%I64d\n", china(5, a, x)); } return 0;}